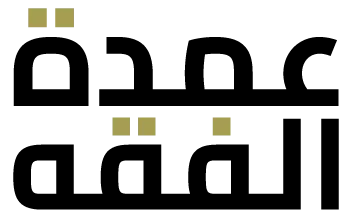The Book of Inheritance

Number of Shares, Redistribution,

Eliminating Fractions, etc

أُصُوْلِ الْمَسَائِلِ ِ

Glossary

The Number of Shares/ Original Denominators ¹¹⁵⁶

The original (denominators/total number of shares) ¹¹⁵⁷ (in all problems of inheritance) are seven: ¹¹⁵⁸
1. When there is one-half, the estate will be divided into 2 shares.
2. When there is one-third or two-thirds, the estate will be divided into 3 shares.
3. When there is one-fourth, alone or with one-half, the estate will be divided into 4 shares.
4. When there is one-eighth, alone or with one-half, the estate will be divided into 8 shares.

:وَهِيَ سَبْعَةٌ
١. فَالنِّصْفُ مِنَ اثْنَيْنِ
.٢.وَالثُّلُثُ وَالثُّلُثَانِ مِنَ ثلاَثَةِ
.٣.وَالرُّبُعُ وَحْدَهُ أَوْ مَعَ النِّصْفِ مِنْ أَرْبَعَةٍ
.٤.وَالثُّمُنُ وَحْدَهُ أَوْ مَعَ النِّصْفِ مِنْ ثَمَانِيَةٍ

Concerning these four, there is never ‘awl. ¹¹⁵⁹

فَهَذِهِ الأَرْبَعَةُ لاَ عَوْلَ فِيْهَا

1156. This is one of the arithmetic topics that are not directly related to fiqh, but they address matters that were important for the jurists to understand to be able to divide estates accurately. Due to the progress in these fields and the presence of advanced calculators and computers, we will not discuss these topics in detail.

1157. What is intended here is to identify the number of shares the estate will be divided by. This number should not have fractions, so if there is 1/2 (a husband’s or daughter’s share, for instance), the estate will be divided into two shares. If there are two shares with each being 1/2 (e.g., a husband and a sister), then each gets one of the two shares (1/2). If there is one entitled to 1/4 and one entitled to 1/3, then we must divide the estate into 12 shares (the least common denominator), so that we can give each one of the heirs their shares without fractions; in this case, the one entitled to 1/3 gets 4/12, and the one entitled to 1/4 gets 3/12.

1158. The agreed upon denominators are those seven: 2, 3, 4, 6, 8, 12, 24. For the madh-habs that give the siblings part of the inheritance in the presence of the grandfather, there are two other denominators (total number of shares) that are used: 18 and 36.

If, along with the one-half, there is also one-third, two-thirds, or one-sixth, then the denominator will be 6. It may be subject to ‘awl, which increases (the denominator) to 10.

.٥.وَإِذَا كَانَ مَعَ النِّصْفِ ثُلُثٌ أَوْ ثُلُثَانِ أَوْ سُدُسٌ، فَهِيَ مِنْ سِتَّةٍ، وَتَعُوْلُ إِلَى عَشَرَةٍ

If, along with the one-fourth, there is any of these three (one-third, two-thirds, or one-sixth), then the (denominator/total number of shares) will be 12. It may be subject to ‘awl, increasing (the denominator) to 17.

.٦ وَإِنْ كَانَ مَعَ الرُّبُعِ أَحَدُ هَذِهِ الثَّلاَثَةِ، فَهِيَ مِنِ اثْنَيْ عَشَرَ، وَتَعُوْلُ إِلَى سَبْعَةَ عَشَرَ.

7. If, along with the one-eighth, there is one-sixth or two-thirds, then the denominator will be 24. It may be subject to ‘awl, increasing (the denominator) to 27.

.٧ وَإِنْ كَانَ مَعَ الثُّمُنِ سُدُسٌ أَوْ ثُلُثَانِ، فَهِيَ مِنْ أَرْبَعَةٍ وَعِشْرِيْنَ، وَتَعُوْلُ إِلَى سَبْعَةٍ وَعِشْرِيْنَ.

1159. ‘Awl may be translated as proportionate reduction because this is what it means in practice. It is done when you have more shares deserved by heirs with designated shares than the shares by which the estate is divided. (In other words, the calculation results in more shares than exist.) For example, if a woman is survived by a husband and two sisters only, the husband is entitled to 1/2 and the sisters to 2/3. However, 1/2 and 2/3 add up to more than the estate. The original denominator of 6 must be increased to 7 to accommodate the designated shares, eventually giving the husband 3/7 instead of 3/6 and the sisters 4/7 instead of 4/6; this amounts to proportionate reduction of all of the shares of the designated-share heirs

Chapter on Redistribution

بَابُ الرَّدِّ

If the designated shares do not exhaust the entire estate, and there are no residuary heirs, the remainder is redistributed among them, except for the spouses, in proportion to their designated shares.

وَإِنْ لَمْ تَسْتَغْرِقِ الْفُرُوْضُ الْمَالَ، وَلَمْ يَكُنْ عَصَبَةٌ، فالباقي يُرَدُّ عَلَيْهِمْ عَلَى قَدْرِ فُرُوْضِهِمْ، إِلاَّالزَّوْجَيْنِ

[Arithmetic Problems of Redistribution]

If they have different designated shares, you take their shares from the original division of their problem and make the number of shares (by which the estate is divided) equal to the number of their shares. ¹¹⁶⁰ If this results in fractions, you multiply that number by their shares. ¹¹⁶¹

فَإِنِ اخْتَلَفَتْ فُرُوْضُهُمْ، أَخَذْتَ سِهَامَهُمْ مِنْ أَصْلِ مَسْأَلَتِهِمْ، ثُمَّ جَعَلْتَ عَدَدَ سِهَامِهِمْ أَصْلَ مَسْأَلَتِهِمْ فَإِنِ انْكَسَرَ عَلَى بَعْضِهِمْ، ضَرَبْتَهُ فِيْ عَدَدِ سِهَامِهِمْ

If there is a spouse, you give his or her shares first, and then you divide the rest of the estate among those heirs who are eligible for redistribution. If there are fractions, you do the corrections for both the new problem of the redistribution-eligible heirs and the original one involving the husband. ¹¹⁶²

وَإِنْ كَانَ مَعَهُمْ أَحَدُ الزَّوْجَيْنِ أَعْطَيْتَهُ سَهْمَهُ مِنْ أَصْلِ مَسْأَلَتِهِ، وَقَسَمْتَ بَاقِيْ مَسْأَلَتِهِ عَلَى مَسْأَلَةِ أَهْلِ الرَّدّ، فإن انْقَسَمَ وإلا ضَرَبْتَ مَسْألة الرَّدِّ في مَسْألَةِ الزَّوْجِ ثُمّ تُصَحَّحُ بعد ذلك على ما سَنَذْكُرُه

1160. Example: If he is survived by a mother and a daughter, the mother is entitled to 1/6 and the daughter to 1/2. The original denominator/total number of shares of the problem is 6, so the mother would take 1/6 and the daughter 3/6. Upon radd, the estate is divided by 4 instead of 6, giving the mother 1/4 and the daughter 3/4.
This is the reverse of ‘awl.

1161. Example: If he is survived by a mother and 3 daughters, the mother gets 1/6, and the three daughters (together) get 2/3. The number of shares here is 6, so the mother would get 1/6 and the three daughters 4/6. The shares in this problem will be reduced to 5, but then 4 shares divided by 3 daughters will result in fractions. To resolve this, you multiply that by 3, making the total number of shares 15, of which the mother gets 3/15 and each of the 3 daughters gets 4/15.

1162. For example: A man is survived by a wife, a mother, and 3 maternal half siblings. His wife takes 1/4, with the mother and siblings taking the remaining 3/4

There is no ‘awl or radd (redistribution) in any case where a residuary heir inherits. ¹¹⁶³

ولَيْسَ في مَسْألَةٍ يَرِثُ فيها عَصَبَةٌ عَوْلٌ ولا رَدٌّ

(through designated shares and redistribution). The mother usually gets 1/6 and the 3 siblings 1/3. So far, the wife gets 1 share, the mother gets 1 share, and the 3 siblings together get 2 shares. However, you cannot divide 2 by 3, so to avoid fractions, you multiply the denominator of the problem of the redistribution-eligible heirs (which is 3) by 3, resulting in a denominator of 9. You give the mother 3 shares and the siblings a total of 6 shares (so 2 each).
At this point, you do not have one denominator for all the heirs (for dividing the estate into equal shares and giving each heir their shares without fractions). To correct the general problem, you multiply 4 (the common denominator of the original problem) x 3 (the original common denominator of the redistribution problem), giving a new denominator of 12. Multiply the wife’s share x 3, so she gets 3/12, and you give the mother 3/12 and each sibling 2/12. (Using computers nowadays can spare us the need for most of the arithmetic problems.)

1163. If the residuary heir inherits, then there is no shortage of the estate to cover the shares of the heirs with designated shares, so there is no ‘awl. Also, the residuary heir inherits the rest of the estate, so there will be nothing left for radd.

Chapter on Eliminating Fractions ¹¹⁶⁴

باَبُ تَصْحِيْحِ اْلمَسَائِلِ

إِذاَ انْكَسَرَ سَهْمُ فَرِيْقٍ عَلَيْهِمْ، ضَرَبْتَ عَدَدَهُمْ، أَوْ وَفْقَهُ إِنْ وَافَقَ سِهَامَهُمْ فِيْ أَصْلِ مَسْأَلَتِهِمْ ، أوْ وَفْقَهُ إِنْ وَافَقَ سِهَامَهُمْ فِيْ أَصْلِ مَسْأَلَتِهِمْ وَعَوْلِهَا إِنْ عَالَتْ، أَوْ نَقْصِهَا إِنْ نَقَصَتْ، ثُمَّ يَصِيْرُ لِكُلِّ وَاحِدٍ مِنْهُمْ مِثْلُ مَا كَانَ لِجَمَاعَتِهِمْ أَوْ وَفْقُهُ ، وَإِنِ انْكَسَرَ عَلىٰ فَرِيْقَيْنِ فَأَكْثَرَ، وَكَانَتْ مُتَمَاثِلَةً، أَجْزَأَكَ أَحَدُهَا ، وَإِنْ كَانَتْ مُتَنَاسِبَةً، أَجْزَأَكَ أَكْثَرُهَا ، وَإِنْ تَبَايَنَتْ ضَرَبْتَ بَعْضَهَا فِيْ بَعْضٍ ، وَإِنْ تَوَافَقَتْ، ضَرَبْتَ وَفْقَ أَحَدِهِمَا فِي اْلآخَرِ، ثُمَّ وَافَقْتَ بَيْنَ مَا بَلَغَ وَبَيْنَ الثَّالِثِ وَضَرَبْتَهُ أَوْ وَفْقَهُ فِيْ الثَّالِثِ، ثُمَّ ضَرَبْتَهُ فِيْ اْلمَسْأَلَةِ، ثُمَّ كُلُّ مَنْ لَهُ شَيْءٌ مِنْ أَصْلِ اْلمَسْأَلَةِ مَضْرُوْبٌ فِي اْلعَدَدِ الَّذِيْ ضَرَبْتَهُ فِي اْلمَسْأَلَةِ

1164. This is another arithmetic topic that can be replaced by our advanced computation tools. Here, Imam Ibn Qudâmah explains how to eliminate the fractions so that every heir gets a share without fractions. For example, the original division gives 2 shares to be split among the maternal half siblings. If we have 7 of them, then each one will get 2/7 of a share. Since this is a fraction, we need to resolve this problem by multiplying the number of shares enough so that each heir gets his/her share(s) without fractions.

Chapter on the Reconstruction of Problems upon the Death of an Heir (al-Munâsakhât) ¹¹⁶⁵

باَبُ اْلمُنَاسَخَاتِ

إِذَا لَمْ تُقْسَمْ تَرِكَةُ اْلمَيِّتِ حَتَّى مَاتَ بَعْضُ وَرَثَتِهِ، وَكَانَ وَرَثَةُ الثَّانِيْ يَرِثُوْنَهُ عَلىٰ حَسْبِ مِيْرَاثِهِمْ مِنَ اْلأَوَّلِ، قَسَمْتَ التَّرِكَةَ عَلىٰ وَرَثَةِ الثَّانِيْ وَأَجْزَأَكَ، وَإِنِ اخْتَلَفَ مِيْرَاثُهُمْ، صَحَّحْتَ مَسْأَلَةَ الثَّانِيْ، وَقَسَمْتَ عَلَيْهَا سِهَامَهُ مِنَ اْلأُوْلىٰ، فَإِنِ انْقَسَمَ، صَحَّتِ اْلمَسْأَلَتَانِ مِمَّا صَحَّتْ مِنْهُ اْلأُوْلى، وَإِنْ لَمْ يَنْقَسِمْ، ضَرَبْتَ الثَّانِيَةَ، أَوْ وَفْقَهَا فِي اْلأُوْلىٰ، ثُمَّ كُلُّ مَنْ لَهُ شَيْءٌ مِنَ اْلأُوْلىٰ مَضْرُوْبٌ فِيْ الثَّانِيَةِ أَوْ وَفْقَهَا، وَمَنْ لَهُ شَيْءٌ فِيْ الثَّانِيَةِ مَضْرُوْبٌ فِيْ سِهَامِ الْمَيِّتِ الثَّانِيْ أَوْ وَفْقَهَا، ثُمَّ تَفْعَلُ فِيْمَا زَادَ مِنَ اْلمَسَائِلِ كَذٰلِكَ

1165. This is another arithmetic topic that can be replaced by our advanced computation tools. Here, Imam Ibn Qudâmah teaches the jurist how to reconstruct the problem if one (or more) of the heirs dies before the distribution of the estate, so their share is passed onto their heirs. Instead of having two different distributions, this chapter allows the heirs of the deceased heirs to be part of the original problem. A simple example on one of the types of reconstruction: A woman dies and is survived by her husband and 1 sister, each of whom will inherit 1/2. The husband dies soon afterwards, so his heirs inherit his 1/2. If he leaves behind 2 sisters and 1 brother, then that 1/2 share (from his wife) will be divided in 4, giving 2 shares to the brother and 1 to each sister. The original problem can be reconstructed to use 8 shares instead of 2, giving the sister of the first deceased 4 shares, the brother of her husband (who died after her) 2 shares, and each of the husband’s sisters 1 share. It is easier, though, to have two different problems, getting the first done with the division of the first problem and then dividing the estate of the second deceased.

Number of Shares, Redistribution, Eliminating Fractions, etc

( Page : no 104)

The Book of Inheritance

Number of Shares, Redistribution,

Eliminating Fractions, etc

أُصُوْلِ الْمَسَائِلِ ِ

Introduction

The Book of Purification

The Book of Prayer

The Book of Funerals

The Book of Fasting

The Book of Hajj and 'Umrah

Book of Zakat

The Book of Selling and Commercial Transactions

The Book of Bequests

The Book of Inheritance

The Book of Marriage

The Book of Divorce

The Book of Sadaq

The Book of Dhihar

The Book of Lian

The Book of Foods

The Book of Oaths

Book of Fatal and Non-Fatal Assault

The Book of Indemnities

The Book of Hudood

The Book of Jihad

The Book of the Judiciary

The Book of Testimonies

Appendix

Glossary

Chapter on Redistribution

بَابُ الرَّدِّ

[Arithmetic Problems of Redistribution]

باَبُ تَصْحِيْحِ اْلمَسَائِلِ

باَبُ اْلمُنَاسَخَاتِ

Number of Shares, Redistribution, Eliminating Fractions, etc